Deep Q-Learning

Felix Christian Lv3
  2025-06-17 15:09:05 2025-06-17 15:09:05 创建   2025-07-14 01:03:31 2025-07-14 01:03:31 更新    6.7k 字  24 分钟  

Q-Learning

思路

回顾一下Q值迭代的公式： 将其写为期望的形式： 在此基础上，Q-Learning的思路就是，通过采样来代替期望：

  1. 获得样本 (Receive a sample): 在当前状态 执行动作 。获得新的状态。

  2. 旧的估计值 (Old estimate): 我们当前对 的估计值是 。

  3. 新的样本估计 (New sample estimate): 它是我们根据刚刚得到的样本，计算出的一个新的、更靠谱的“目标价值”。注意，这个式子和第一步公式括号里的内容一模一样，但它使用的 R 和 s′ 是我们刚刚实际观测到的，而不是一个理论上的期望值。

  4. 增量更新 (Incorporate the new estimate): 这是最终的Q-Learning更新公式。我们不会用新的目标值 完全覆盖掉旧的估计值，而是像“微调”一样，把旧值向新目标值“拉”一点点。

  • α (alpha) 是学习率 (learning rate)，一个0到1之间的小数。它控制了我们每一步更新的幅度。
  • 如果 α=0：我们完全不学习，Q值永远不变。
  • 如果 α=1：我们完全抛弃旧值，用新的Target代替，这通常会导致学习过程不稳定。

流程

算法具体流程如下：

    • Algorithm: (算法流程)：

      1. Start with for all
        • 在算法开始时，我们需要创建一个表格，用来存储所有“状态（state）”和“动作（action）”组合的值。
      2. Get initial state
        • 开始一轮学习（一个 episode）。把智能体放在环境中的一个起始位置 。
      3. For till convergence
        • 这是学习的核心循环。智能体会不断地与环境交互，更新表，这个过程会重复成千上万次（是步数计数器)，直到表中的值收敛。
      4. Sample action , get next state
        • 在当前状态，智能体需要选择一个动作来执行。通常使用 -greedy (epsilon-greedy)策略：
          • 有 的概率，选择当前状态下值最大的动作（利用现有知识）。
          • 有 的概率，随机选择一个动作（探索未知可能）。
        • 执行动作后，环境会给出一个反馈：智能体进入了下一个状态，并获得一个奖励（奖励在下一步的 target 计算中用到）。
      5. If is terminal:
          • 如果是终止状态，我们的目标值 $target$ 就是获得的最后那个奖励 。
        • Sample new initial state : 当前这轮（episode）结束了，让智能体重新回到一个起始位置，准备开始新的一轮。
      6. else:
          • 尚未终止。我们用上面提到的公式来计算目标值。
        • 这是整个算法最核心的更新步骤。无论 if 还是 else，我们都用计算出的 $target$ 来更新原始状态动作对 的值。我们用学习率 把旧的值向新的 $target$ 值“拉拢”一点。
        • 智能体已经移动到了新的状态。我们把设为当前状态，然后返回第4步，开启下一次“选择动作 -> 观察结果 -> 更新值”的循环。

特性

核心概念：离策略 (Off-Policy) 学习

  • 定义： “行动”的策略和“学习”的策略可以不一样。
  • 表现： 即使智能体为了探索而做出“非最优”的随机动作，它学习到的依然是“最优”的路径。

收敛的3个前提条件 (Caveats):

  • 充分探索： 必须尝试足够多的状态和动作，避免漏掉最优解。
  • 学习率(α)最终要小： 保证Q值后期能稳定收敛，不剧烈波动。
  • 学习率(α)不能降太快： 防止Q值在学好之前就提前“定型”，不再更新。

用更严谨的表达：

1. 充分探索 (Infinite Visitation)：

  • All states and actions are visited infinitely often
    • 含义： 所有的状态和动作对 (s,a) 都必须被访问无限次。
    • 解释： 这是对“充分探索”的严格数学定义。在理论证明中，需要“无限次”来保证无论初始的Q值有多差，最终都有机会被修正过来。在实际应用中，这意味着每个 (s,a) 对都要被访问非常非常多次。
  • Basically, in the limit, it doesn't matter how you select actions (!)
    • 含义： 从极限的角度看，你具体如何选择动作其实不重要！
    • 解释： 这是一个非常深刻的结论。它指的是，只要你的动作选择策略能保证“无限访问”这个条件，那么无论是用ε-greedy，还是其他更复杂的探索方法，最终Q-Learning都能收敛到最优策略。因为Q-Learning更新公式中的 max 操作会持续地将Q值推向最优的方向，时间长了，探索时产生的“噪音”就会被淹没。

2. 学习率设定条件 (Learning Rate Schedule)： 这里用两个数学公式，精确地定义了上面我们讨论的“学习率(α)要变小，但不能太快变小”。这里的 指的是在时间步 时，用于更新 对的学习率。

    • 数学含义： 所有学习率从头到尾加起来的总和，必须是无穷大。
    • 直观解释： 这个条件保证了学习不会过早停止。你可以把学习率想象成你前进的“步长”。这个公式要求你所有步长加起来的总距离是无限的。这意味着，无论你离目标有多远，只要一直走下去，就一定能到达。如果这个总和是有限的，比如总共只能走100米，那如果你的目标在101米外，你就永远也走不到了。这对应了“学习率不能降太快”的规则。
    • 数学含义： 所有学习率的平方加起来的总和，必须是一个有限的数（即收敛）。
    • 直观解释： 这个条件保证了学习最终会稳定下来。它要求你的“步长”最终必须趋向于0，并且要足够快地趋向于0。这样，在学习的后期，每次更新的幅度会变得非常小，Q值才不会因为某次随机的、不好的采样而大幅波动，从而能够稳定在最优值附近。这对应了“学习率最终要足够小”的规则。

局限

表格方法局限性 点击展开查看

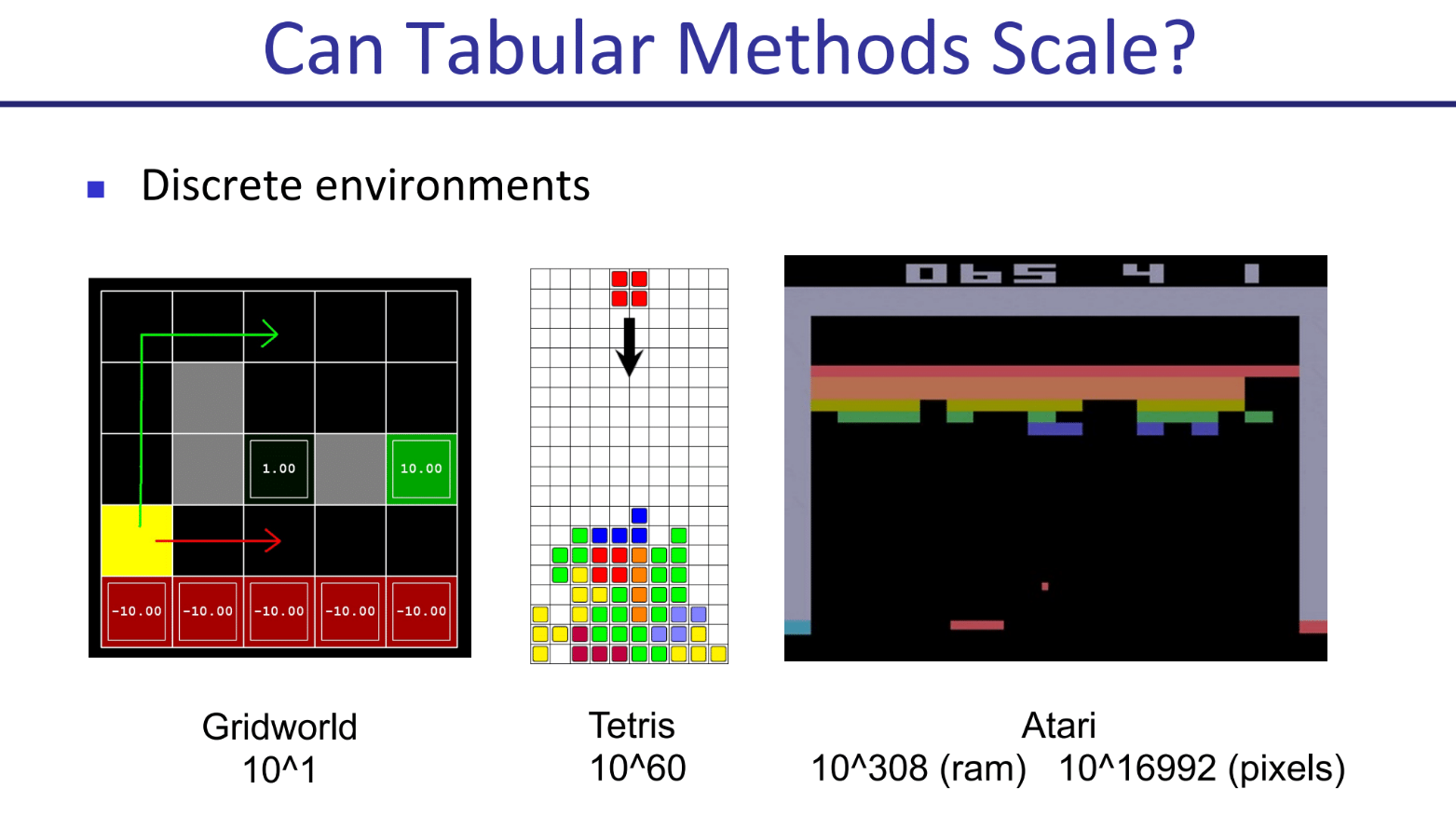
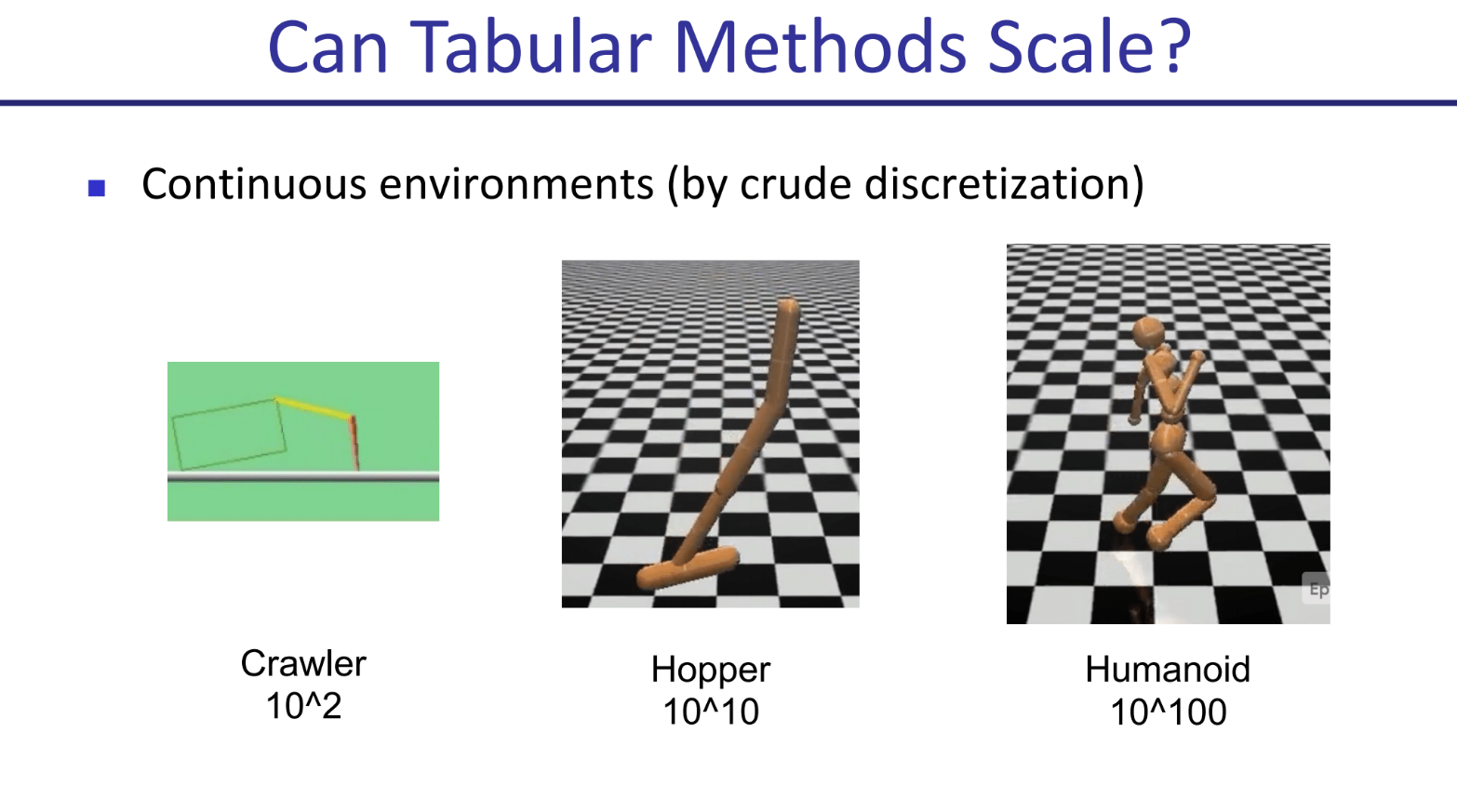
核心问题：状态空间爆炸 (State Space Explosion)

我们之前讲的Q-Learning，核心是那张 Q表 (Q-Table)。它要求我们为环境中的每一个可能的状态都分配一行来记录Q值。

对于非常简单的环境，这是可行的。但是一旦环境变得复杂，状态的数量会增长得极其恐怖，这个现象也叫 “维度灾难” (Curse of Dimensionality)。

图中例子可以看出，即使在状态是离散的环境中，状态数量也会暴增。在连续状态（比如机器人关节的角度、速度）的环境中，问题甚至更严重。

In realistic situations, we cannot possibly learn about every single state!

  • 在现实复杂问题中，我们不可能学习完所有状态。原因有二：
    1. 没时间访问所有状态 (Too many states to visit): 在训练中，要把像Atari游戏里的每一种可能的游戏画面都经历一遍，需要的时间是天文数字。
    2. 没内存存储所有状态 (Too many states to hold): 就算有时间，我们的计算机也存不下一张包含万亿、亿亿行的Q表。

为了解决状态空间爆炸问题，核心思想是进行泛化(Generalization)。

做法：

  1. 从少量经验中学习 (Learn about some small number of training states): 智能体只从它在训练中实际遇到过的那些状态中学习。
  2. 将经验推广到新情况 (Generalize that experience to new, similar situations): 这是最关键的一步。模型需要能够根据已有的经验，对从未见过但很相似的状态做出合理的价值判断。

优化

近似Q学习（Approximate Q-Learning)：

我们不再使用一张巨大的Q表来存储每一个状态-动作对的值，而是使用一个带有参数的函数 来计算（或近似）这个值。

  • 函数可以是多种形式：
    1. 线性函数 (Linear function in features):
    2. 神经网络 (neural net), 决策树 (decision tree), etc.

新的学习规则 (Learning rule)：

既然没有表格了，我们的更新方式也变了。我们不再更新表格中的一个单元格，而是更新函数的参数 θ。这个更新过程使用的是梯度下降法 (Gradient Descent)。

  1. 目标值 (target) 的计算:
  2. 更新参数 θ:
    • 我们来分解这个公式：
      • 误差 (Error): 是我们当前函数的预测值与目标值之间的差距。
      • 损失函数 (Loss Function): 我们将误差平方 (error)²，这得到了一个永远为正的“损失值”。我们的目标就是让这个损失值变得尽可能小。
      • 梯度 (∇): 这是微积分中的一个符号，表示“梯度”。梯度指向的是函数值增长最快的方向。所以，损失函数的梯度就指向了让损失值增大的方向。
      • 梯度下降: 我们在梯度的前面放一个负号 (- α∇...)，就意味着我们要让参数 θ 沿着损失值下降最快的方向进行调整。α 是学习率，控制着每一步调整的幅度大小。

Deep Learning / Neural Networks

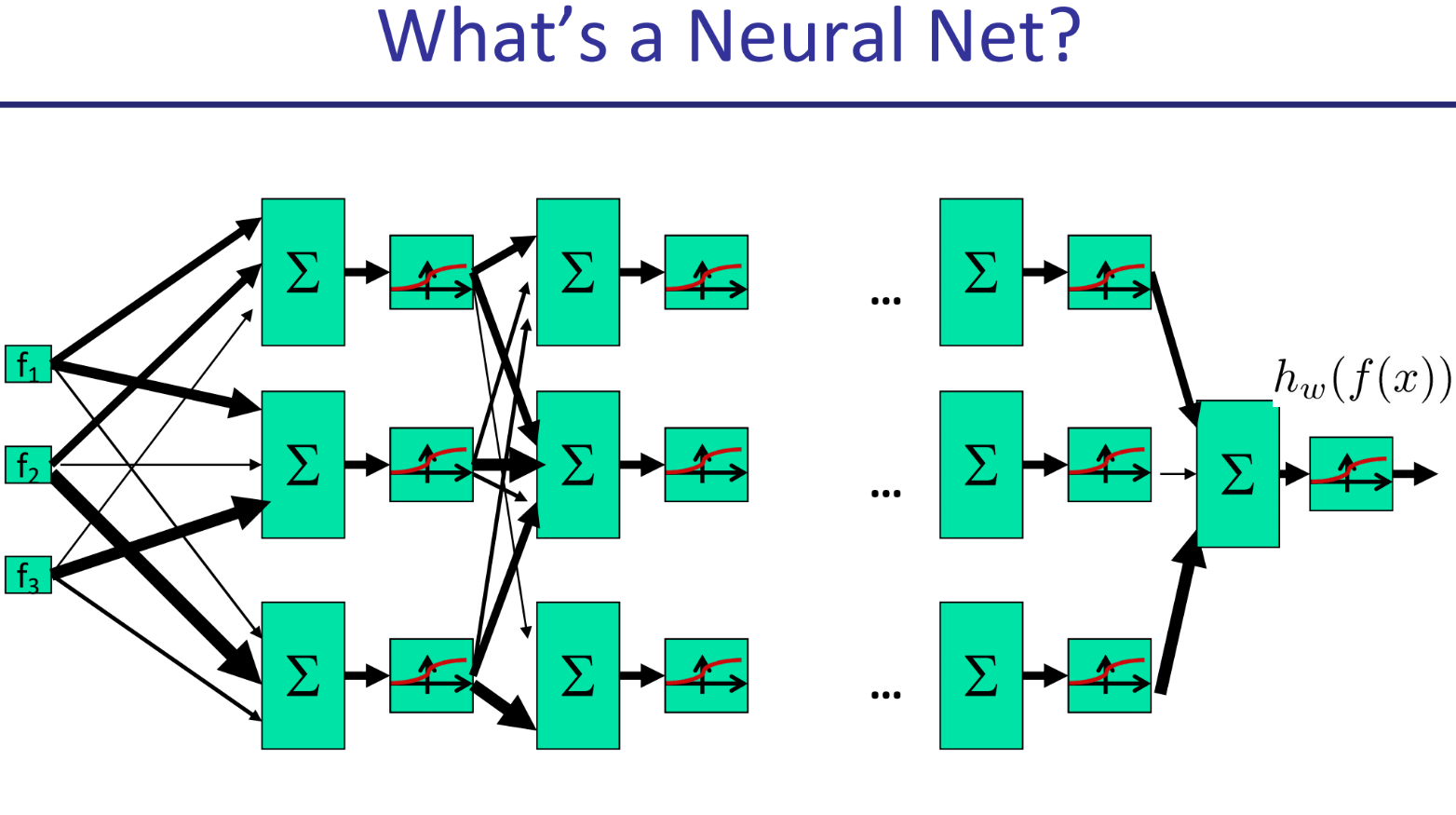
神经网络

简单来说，神经网络通过将许多简单的计算单元（神经元）分层排列，来处理和转换信息。

  1. 输入特征 (f1,f2,f3)
    • 这是网络的输入层，代表了提供给模型的信息。在强化学习中，这可能就是描述当前状态的特征。
  2. 箭头和线条粗细
    • 箭头表示数据的流动方向，从左到右。
    • 线条的粗细代表了连接的权重 (Weight)。粗线条表示这个连接的权重值很大，意味着前一层这个节点对后一层节点的影响力更强。这些权重就是神经网络需要学习的参数 W 或 θ。
  3. 计算单元（方框内的符号）
    • 求和框 (Σ): 代表线性变换。每个神经元会把它所有输入信号根据连接的权重进行加权求和。
    • 激活函数框 (S形曲线): 代表非线性激活。上一步加权求和的结果会经过一个非线性函数（如图中的S形函数，或上一页的ReLU函数）进行处理。这一步至关重要，它赋予了网络学习复杂模式的能力。

分层结构

  • 隐藏层 (Hidden Layers):
    • 输入层和输出层之间的所有层都叫隐藏层。数据从输入层开始，逐层向后传递。
    • 每一层都会对前一层输出的结果进行新的“加权求和 + 激活”计算，从而提取出更高级、更抽象的特征。第一层可能只能识别简单的模式，而更深的层可以组合这些简单模式，以识别更复杂的概念。
  • 输出层 (Output Layer):
    • 网络的最后一层，它会给出最终的计算结果。

多层感知机 (MLP)

MLP的关键在于，它在每一层线性变换之后，都会插入一个非线性的激活函数 (activation function)。这个“非线性”是赋予神经网络强大能力的核心。

激活函数：

一个直观的MLP结构：

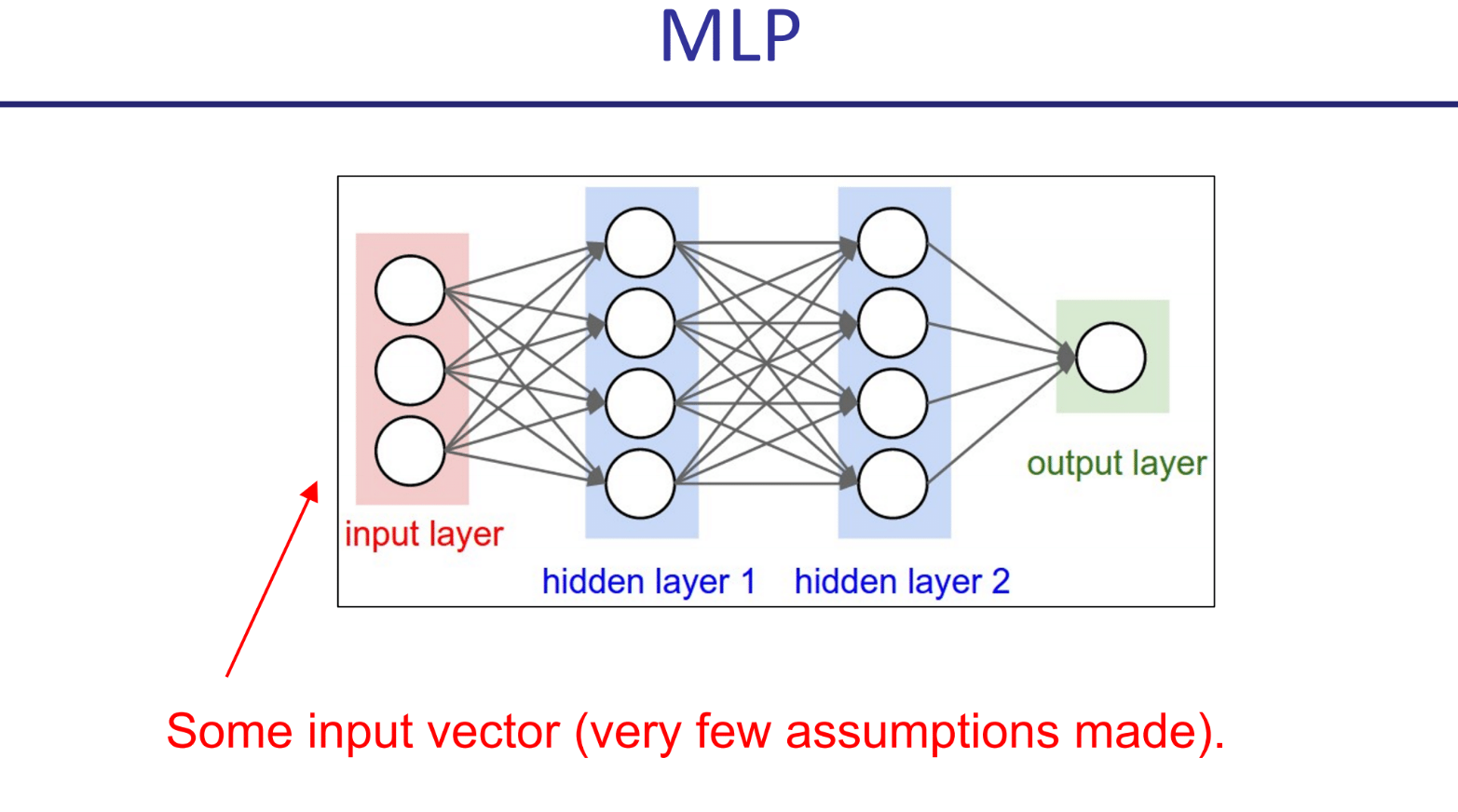
卷积神经网络(CNN)

CNN的核心思想

普通的MLP（多层感知机）在处理图像时，会先把图像像素拉成一个长长的一维向量，这会破坏图像固有的空间结构（比如，哪些像素是相邻的）。

CNN专门为处理像图像这样的网格状数据而设计。它不关注单个像素，而是通过“卷积核”来观察局部区域，寻找并识别像边缘、角点、纹理这样的局部模式。

这张图展示了一个典型的CNN架构，从左到右处理一张汽车图片：

  1. 输入 (Input):
    • 左侧的汽车图片。
  2. 特征提取部分 (多个CONV RELU POOL模块):
    • 这一长串的模块是CNN的精髓，负责从图像中逐层提取特征。
    • CONV (卷积层):
      • 这是CNN的核心。它使用许多小的“滤波器”或“卷积核”（可以想象成一个个小小的放大镜）在整个图像上滑动。
      • 每个滤波器专门负责检测一种特定的局部特征。
      • 卷积层处理完后，会输出一系列“特征图”（Feature Maps），也就是图中那些小小的黑白图片。每一张特征图都显示了它所对应的那个特定特征在原图的哪些位置出现了。
    • RELU (激活函数):
      • 和我们之前讨论的一样，它在卷积操作后增加非线性，增强网络的表达能力。
    • POOL (池化层):
      • 主要作用是降采样或压缩特征图的尺寸。最常见的是“最大池化”（Max Pooling），它在一个小窗口（比如2x2区域）内只保留最大的那个值。
      • 好处： 1. 减少计算量； 2. 让模型对特征在图像中的微小位置变化不那么敏感，增强模型的鲁棒性。
  3. 分类部分 (FC层):
    • FC (全连接层 - Fully Connected Layer):
      • 在经过多轮“卷积-激活-池化”的特征提取后，最终得到的复杂的特征图会被“压平”成一个长长的一维向量。
      • 这个向量随后被送入一个我们已经熟悉了的普通MLP（全连接层就是MLP）中。
      • 这个MLP负责根据提取出的高级特征，进行最终的分类或决策。
  4. 输出 (Output):
    • 网络的最后一层输出对每个类别的评分。图中，"car"（汽车）这个类别的得分最高，因此网络正确地识别出了图片内容。
优化 点击展开查看

好的，这张图讲解的是优化（Optimization），即在实际中我们如何调整神经网络的参数（θ）来让它的表现变得更好。

1. 这是一个非凸问题 (Non-convex problem)

  • 含义： 神经网络的损失函数（我们要最小化的那个误差函数）通常是一个非凸函数。
  • 直观理解：
    • 凸问题：像一个光滑的碗。无论你从碗的哪里开始，只要一直往下走，最终总能到达唯一的最低点（全局最优解）。
    • 非凸问题：像一个坑坑洼洼、有许多山谷和山峰的复杂地形。你很容易顺着坡走到某一个山谷的谷底（一个局部最优解），但这个谷底不一定是整个地形的最低点。
  • Gradient-based methods are surprisingly effective
    • 含义： 尽管理论上存在会卡在“局部最优”的风险，但在实践中，基于梯度的方法（比如我们之前讨论的梯度下降）在训练大型神经网络时出奇地有效。这至今仍然是深度学习研究中的一个热门话题。

2. 如何计算梯度 (How to Compute Gradients)

  • Minibatch stochastic gradients instead of full gradient
    • 含义： 我们不使用整个数据集来计算梯度，而是使用“小批量随机梯度”。
    • 对比三种方式：
      1. Full Gradient (批量梯度下降): 用全部训练数据计算一次梯度。优点是方向准，缺点是数据量大时计算极其缓慢，内存开销大。
      2. Stochastic Gradient (随机梯度下降): 随机选一个数据点计算一次梯度。优点是速度飞快，缺点是方向很不稳定。
      3. Minibatch Gradient (小批量梯度下降): 这是两者的折中，也是最常用的方法。我们一次用一小批数据（如32, 64, 256个样本）来计算梯度。这样既保证了计算效率，又使得梯度的方向相对稳定。

3. 梯度的自动计算 (Automatic Differentiation)

  • Gradient calculation done by Automatic differentiation
    • 含义： 像神经网络这么复杂的函数，它的梯度公式手算是完全不现实的。幸运的是，计算机可以帮我们自动完成。
  • Learn backpropagation (学习反向传播算法)
    • 反向传播 (Backpropagation) 是实现自动微分的核心算法。它利用微积分中的“链式法则”，从网络的输出层开始，一层一层地向后计算出损失函数相对于网络中每一个参数（权重）的梯度。它是训练神经网络的引擎。
  • Use a deep learning framework...
    • 含义： 在实践中，我们不需要自己从零开始写反向传播算法。像 Tensorflow, PyTorch 这样的深度学习框架已经内置了自动微分功能。我们只需要负责搭建神经网络（前向传播），框架会自动帮我们计算所有梯度。

4. 最常用的优化器 (Most Common Optimizers)

  • SGD + Momentum + Preconditioning
    • 含义： 朴素的（小批量）随机梯度下降法（SGD）虽然能用，但通常我们会使用一些更高级的“优化器”来加速和稳定训练过程。
    • Momentum (动量):
      • 思想： 模拟一个从山上滚下来的球。这个球不仅受当前坡度的影响，还带有自身的惯性。这可以帮助它冲过一些小的颠簸（局部最优），并且在坡度方向一致的区域加速下降。
    • Preconditioning (或称 Adaptive Learning Rates, 自适应学习率):
      • 思想： 为网络中的每一个参数设置不同的、可自适应调整的学习率。比如，对于不经常更新的参数，我们给一个较大的学习率；对于频繁更新的参数，我们给一个较小的学习率。
  • Try RMSProp, Adam, Adamax...
    • 这些就是集成了上述思想的流行优化器算法的名字。
    • Adam (Adaptive Moment Estimation) 是目前最常用、最受欢迎的优化器之一，因为它同时结合了动量和自适应学习率的优点，通常能快速且稳定地得到好结果。在不确定用什么优化器时，Adam通常是一个优秀的首选项。

Deep Q Networks(DQN)

流程

好的，上图展示的是则是DQN训练算法的流程。

这个算法的核心是在我们之前讨论的近似Q学习的基础上，加入了两个关键的创新点：经验回放 (Experience Replay) 和 固定Q目标 (Fixed Q-Targets)，也叫目标网络。

初始化阶段

  1. Initialize replay memory D to capacity N
    • 含义： 初始化一个固定容量为N的“经验回放池” D。这个N可以很大，比如100万。
    • 作用 (经验回放): 这是DQN的第一个关键创新。智能体不再是“现学现卖”（用完一个经验就扔掉），而是把经历过的所有事情（状态、动作、奖励等）都存到这个池子里。学习的时候，随机从池子里抽取一小批经验来学习。
  2. Initialize action-value function Q with random weights θ
    • 含义： 初始化我们主要的Q网络，也叫“在线网络”（Online Network），其参数为 θ。
  3. Initialize target action-value function Q_hat with weights θ⁻ = θ
    • 含义： 创建一个结构完全相同，参数也完全一样的“目标网络”（Target Network）。
    • 作用 (固定Q目标): 这是DQN的第二个关键创新。在之前的算法中，计算目标值y和计算预测值都用的是同一个网络Q，这相当于“追逐一个移动的目标”，会导致训练非常不稳定。DQN用这个独立的、参数被“冻结”的目标网络来计算目标值，使得学习目标在一段时间内是固定的，从而大大增加了训练的稳定性。

主训练循环

  • For episode = 1, M do / For t = 1, T do: 对每一episode中的每一步进行循环。
  • 与环境交互
    1. 选择动作: 使用在线网络Q和ε-greedy策略选择一个动作。
    2. 执行动作: 在环境中执行动作，得到奖励和下一帧图像。
    3. 存储经验: 将这次的完整经验 (当前状态, 动作, 奖励, 下一状态) 存入经验回放池D中。
  • 从经验中学习
    1. 采样: 从经验池D中随机抽取一小批（minibatch）经验。
    2. 计算目标值y:对抽样出的每一条经验，使用目标网络 来计算目标值 。
      • ⁻
      • 注意： 这里用的是参数为 θ⁻ 的目标网络，它的参数是旧的、被冻结的，所以y_j的值是稳定的。
    3. 执行梯度下降:
      • 计算“目标值”和“在线网络Q的预测值”之间的误差。
      • 根据这个误差，计算梯度并更新在线网络的参数θ。
  • 更新目标网络
    • Every C steps reset Q_hat = Q: 每隔C个训练步（比如10000步），才把在线网络的最新参数θ复制给目标网络，更新θ⁻。这确保了目标网络在大部分时间内是稳定的，只进行周期性的更新。

细节

1. 使用Huber损失函数 (Huber Loss)

DQN在计算误差时，没有使用我们之前提到的简单平方损失 (error)²，而是使用了Huber损失。

  • 它是什么？ Huber损失是一个“混合”损失函数，结合了平方损失和绝对值损失的优点。
    • 当误差a（即 y - Q(s,a)）很小时（∣a∣≤δ），它的计算方式和平方损失一样。
    • 当误差a很大时（∣a∣>δ），它的计算方式变为线性增长，类似于绝对值损失。
  • 为什么使用它？ 在强化学习的初期，Q网络的预测可能非常不准，导致计算出的误差a非常大。如果使用平方损失，这个巨大的误差会被平方，导致一个极其夸张的梯度，可能使网络更新“跑偏”，让训练变得非常不稳定。Huber损失对这种大的“离谱”误差惩罚更温和（线性增长而非平方增长），从而让训练过程对异常值不那么敏感，整体更加稳定、鲁棒。

2. 使用RMSProp优化器

DQN使用了RMSProp优化器，而不是基础的随机梯度下降（vanilla SGD）。

  • 它是什么？ RMSProp是一种自适应学习率的优化器。它会为网络中的每一个参数独立地调整学习率。
  • 为什么使用它？ 选择一个合适的优化器对强化学习至关重要。像RMSProp这样的自适应优化器通常比基础的SGD收敛得更快、更稳定，能更好地处理强化学习中奖励稀疏、梯度变化大的问题。

3. 探索率退火 (Anneal the exploration rate)

这里描述了DQN中 ε-greedy 策略的ε值是如何随时间变化的，这个过程叫做“退火”。

  • 它是什么？ “退火”意味着ε的值会随着训练的进行而逐渐减小。
  • 具体策略：
    • 训练开始时，设置 ε = 1。
    • 在训练的前一百万步内，将ε的值线性地从1逐渐降低到一个很小的值，比如0.1或0.05。
    • 之后，ε保持在这个小值上。
  • 为什么这么做？ 这是一种经典的“先探索，后利用”的策略。
    • 初期 (ε = 1)： 此时智能体对环境一无所知，Q值是随机的。设置ε = 1意味着它会完全随机地行动，从而最大化地探索环境，收集多样化的经验。
    • 后期 (ε = 0.1): 随着学习的进行，智能体的Q函数越来越准确。降低ε的值，使得它更多地利用已学到的知识来选择最优动作，而不是随机乱撞。保留一个很小的ε值是为了确保智能体永不停止探索，以防当前策略并非完美。
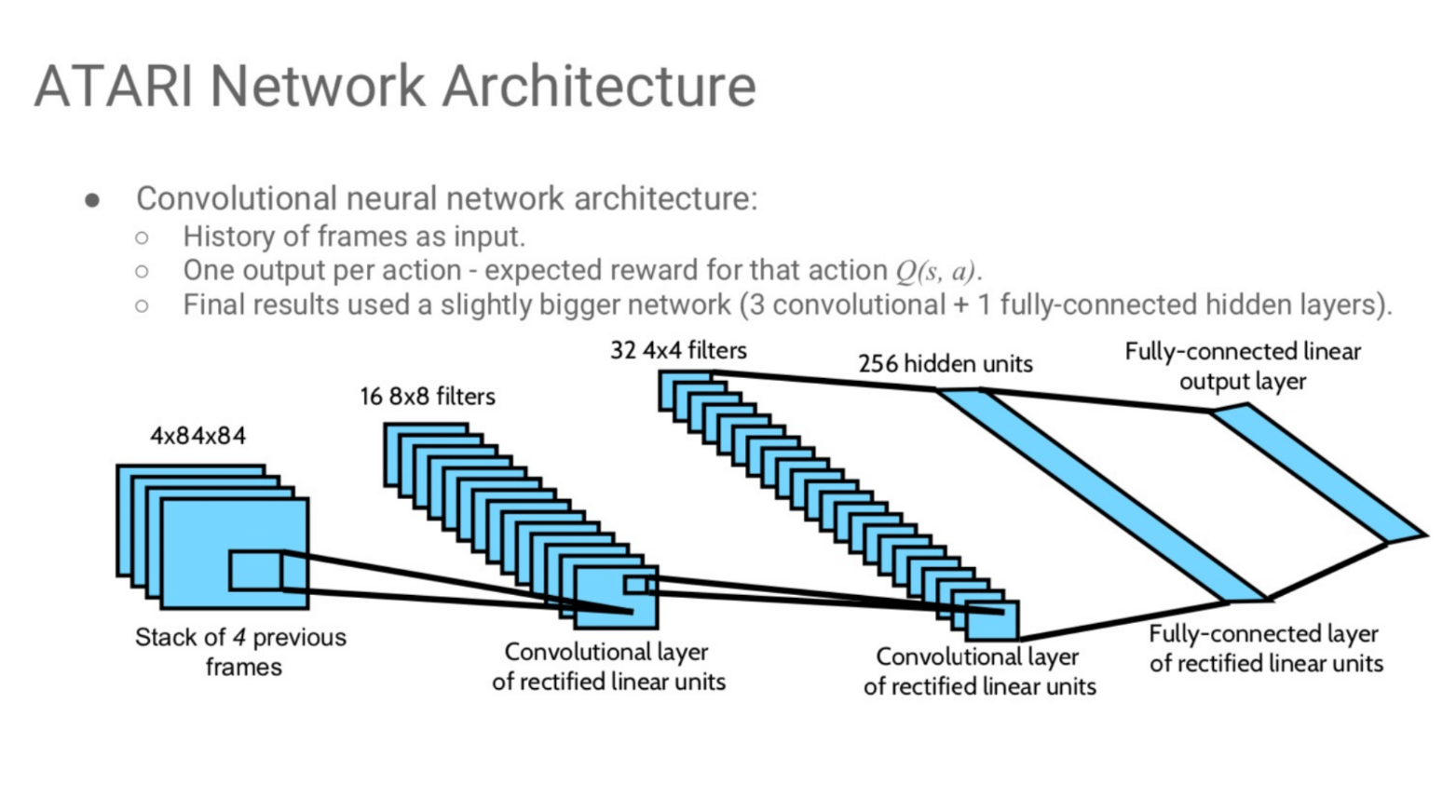
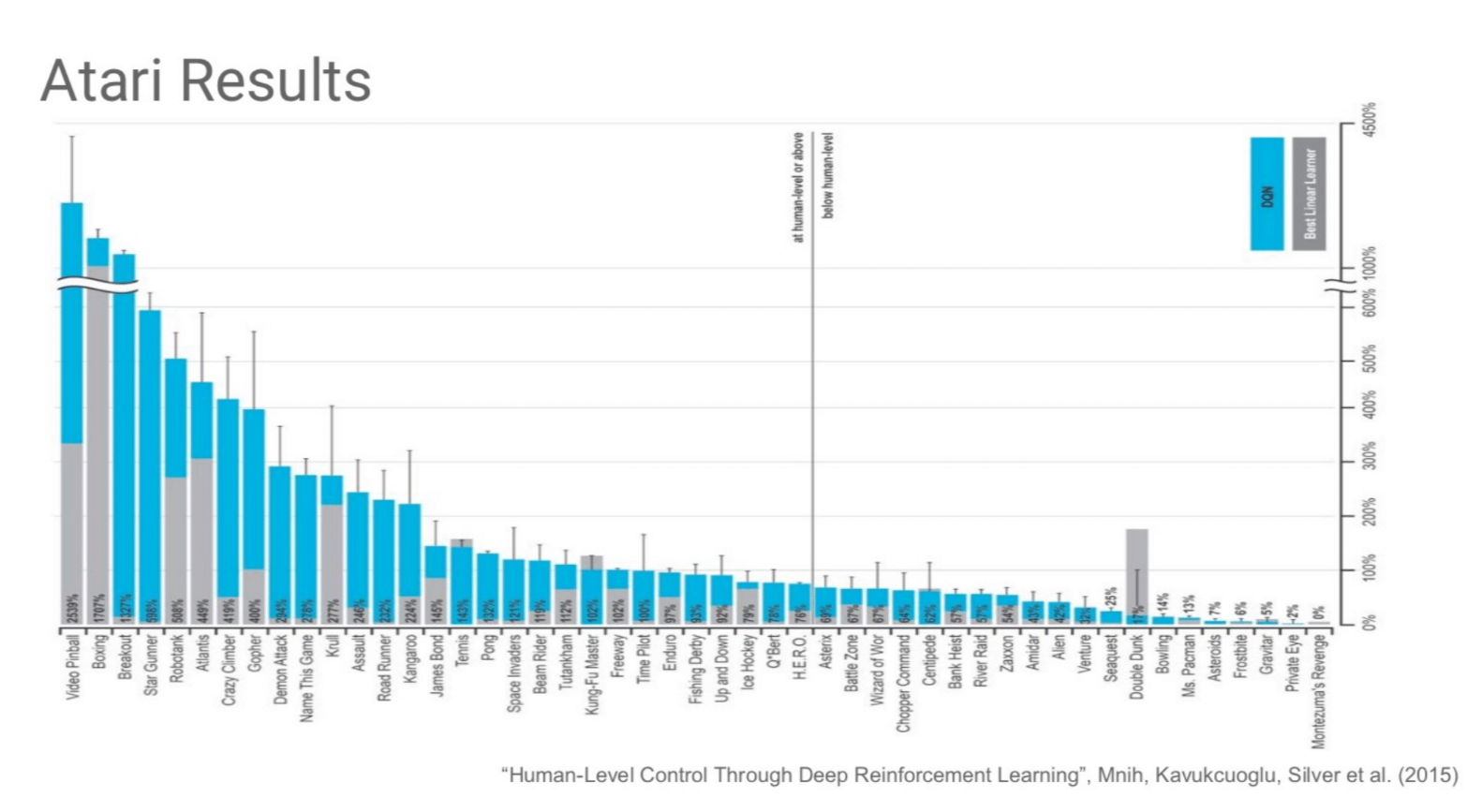
DQN示例-ATARI 点击展开查看

改进

1. 双重深度Q网络 (Double DQN, DDQN)

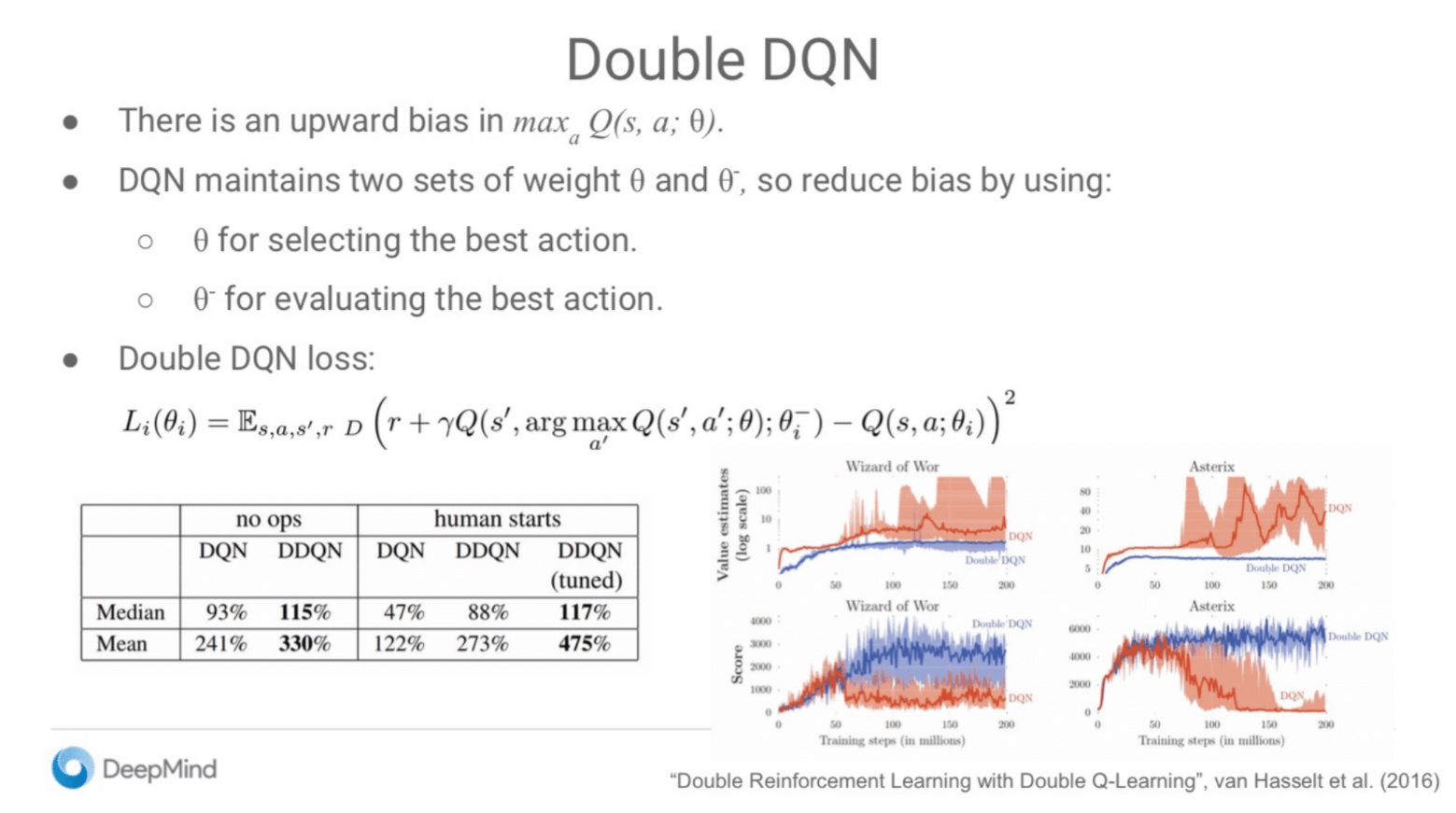
DQN的问题：过度估计 (Overestimation)

  • There is an upward bias in max Q(s, a; θ)
    • 问题： 标准的DQN算法在计算目标值时，存在一个系统性的“过度估计偏差”。也就是说，它倾向于高估动作的Q值。
    • 原因： 在计算目标值 ⁻时，max操作会选择并评估下一状态中Q值最大的那个动作。如果某个动作的Q值因为随机误差而被偶然高估了，max操作就会选中它，导致这个被高估的值被用于计算目标y。这种机制会系统性地将Q值越推越高，使其偏离真实值，影响策略的质量。

Double DQN的解决方案：解耦“选择”与“评估”

Double DQN的核心思想非常巧妙：将“选择最佳动作”和“评估该动作的价值”这两个步骤分离开，使用不同的网络来执行。

  • θ for selecting the best action
    • 使用在线网络 (Online Network)，也就是参数为θ的那个网络，来选择下一状态s'中哪个动作是最好的。
  • θ⁻ for evaluating the best action
    • 使用目标网络 (Target Network)，也就是参数为θ⁻的那个网络，来评估上一步选出的那个动作的价值究竟是多少。

这样一来，即使在线网络θ对某个动作的价值产生了高估并选中了它，我们仍然会用更稳定、独立的的目标网络θ⁻来给出它的价值。因为两个网络产生相同高估的可能性很小，所以整体的过度估计偏差就被大大降低了。

Double DQN的损失函数 (The Loss)

目标值y的计算公式：

损失函数则是通过计算目标值和预测值的差距获得的：目标值预测值

2. 优先经验回放 (Prioritized Experience Replay, PER)

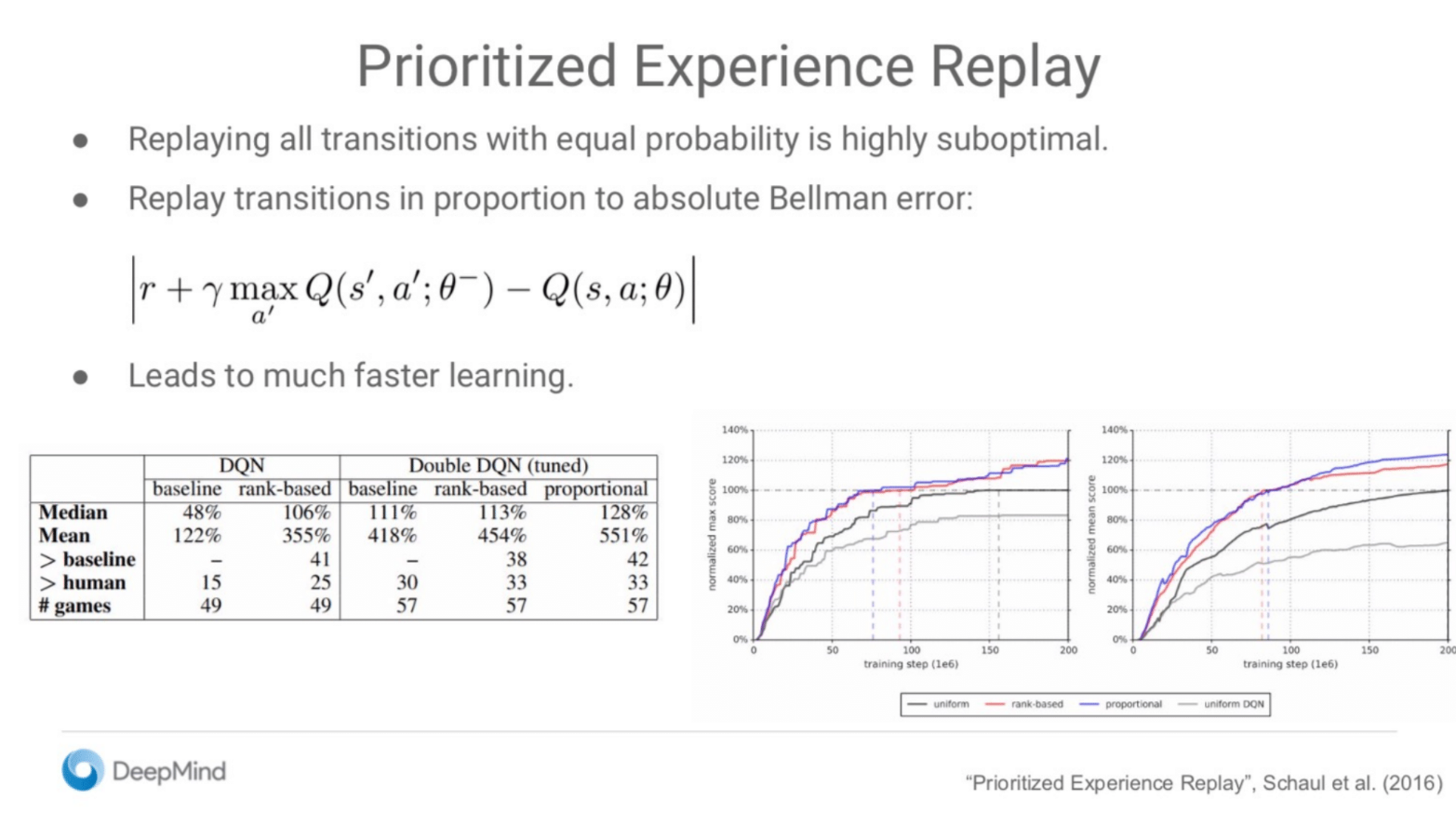
Replaying all transitions with equal probability is highly suboptimal.

标准的经验回放机制（从经验池中完全随机地抽样）是次优的。

Replay transitions in proportion to absolute Bellman error

核心思想： 我们应该优先回放那些能让我们学到最多东西的经历。

如何衡量“学习价值”？ PER使用TD误差（TD-error）的大小来衡量一次经历的“意外程度”或“学习价值”。 目标值预测值直观理解：

  • TD误差大： 意味着“预测”和“实际结果”差距很大。这说明经历非常“出乎意料”，智能体能从中学到很多，因此赋予它很高的优先级。
  • TD误差小： 意味着“预测”和“实际结果”基本相符。这说明经历在预料之中，能学到的东西不多，因此赋予它较低的优先级。

具体做法： 在从经验池中抽样时，不再是完全随机，而是根据这个优先级来抽样，优先级越高的经历被抽中的概率越大。

PER会使学习效率大幅提升。

  • 标题: Deep Q-Learning
  • 作者: Felix Christian
  • 创建于 : 2025-06-17 15:09:05
  • 更新于 : 2025-07-14 01:03:31
  • 链接: https://felixchristian.top/2025/06/17/17-DeepRL_lecture2/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
Deep Q-Learning
  1. Q-Learning
    1. 思路
    2. 流程
    3. 特性
    4. 局限
    5. 优化
  2. Deep Learning / Neural Networks
    1. 神经网络
    2. 多层感知机 (MLP)
    3. 卷积神经网络(CNN)
  3. Deep Q Networks(DQN)
    1. 流程
    2. 细节
    3. 改进