MDPs and Exact Solution Methods
一、马尔科夫决策过程(MDPS)
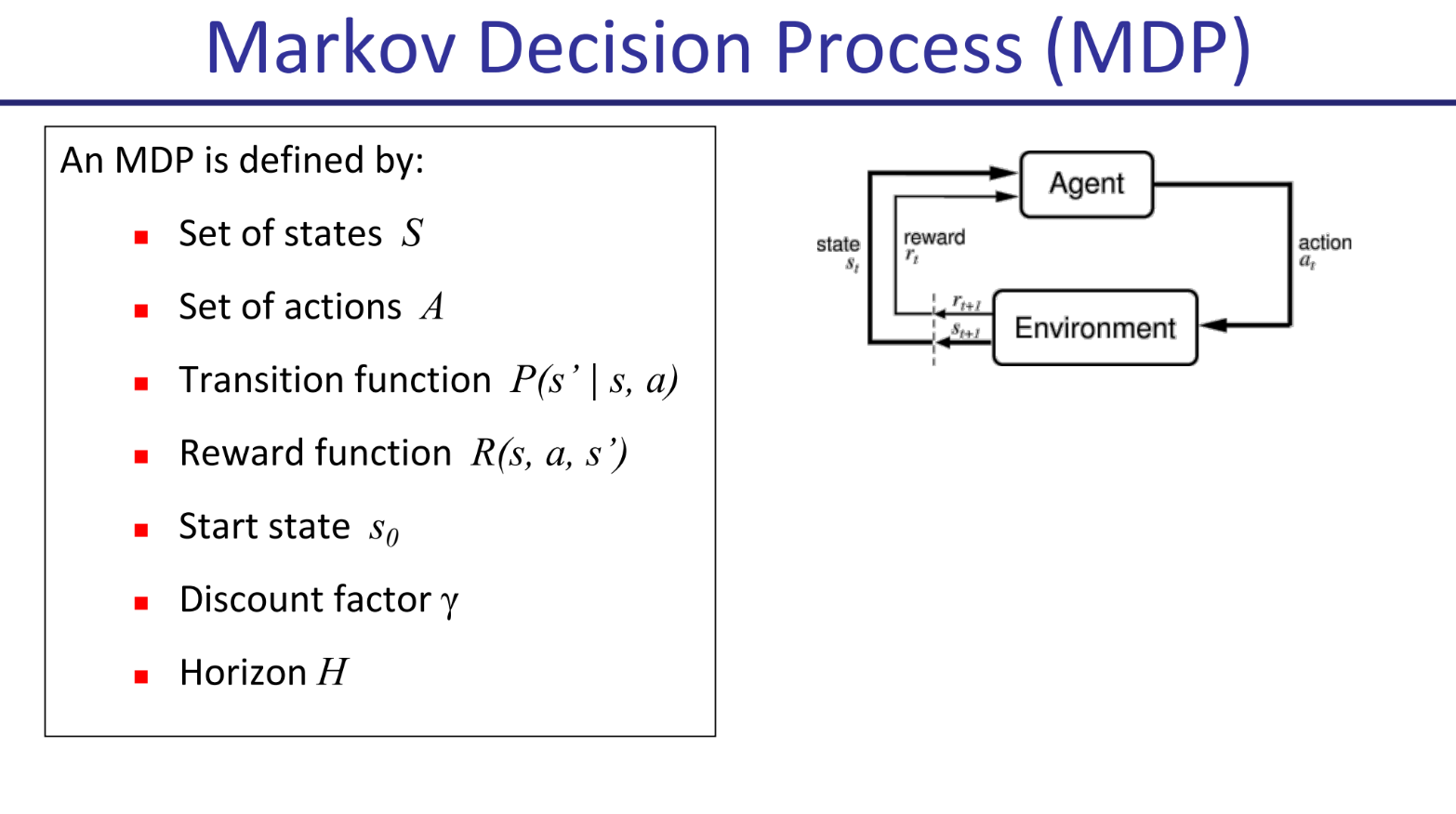
MDP定义:
:智能体的状态集合。 :智能体可以选择的行动集合。 :转变函数,定义智能体当前状态为 ,采取动作 ,进入状态 的概率。 :奖励函数,为上述转变分配奖励。 :初始状态。 :折扣因子,对未来奖励的折扣。 :范围,智能体行动的时间。
MDP求解:
在一个MDP中,我们想要找到一个最优的策略(policy)
- 对于一个给定的状态和时间,策略
给出一个行动。 - 最优策略指能使奖励的期望最大的策略。
如果环境是确定的,那么只需要一个最优的plan,即一系列的行动,从起始点到终点。
二、精确求解方法
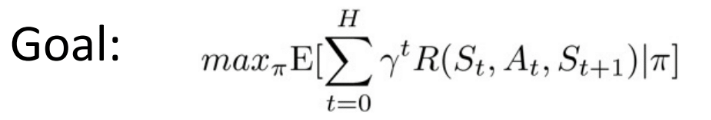
目标:最大化随时间累计,折扣后奖励总和的期望值。
(一)、值迭代
最优值方程:
从状态
示例 点击展开查看

算法:
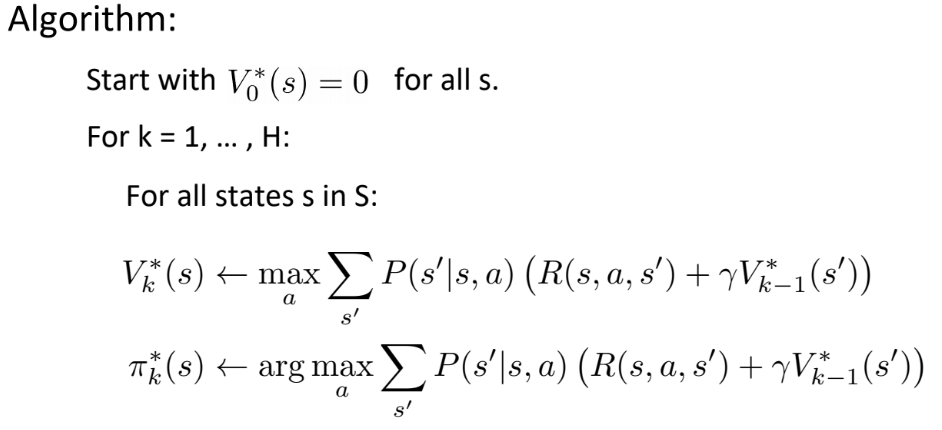
示例 点击展开查看
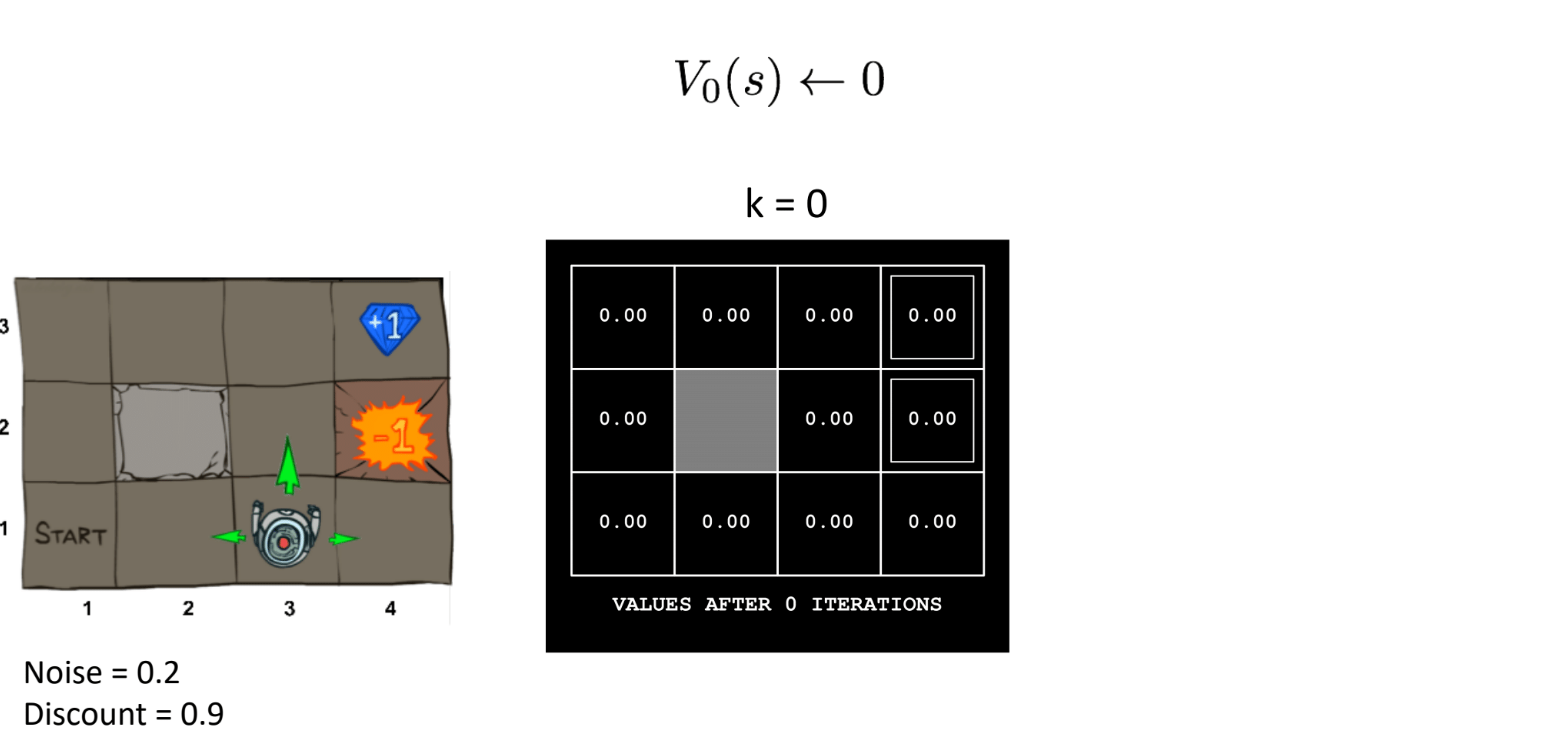
注意这个机器人朝向,三个箭头说明一次行动中只有三个可能的方向(这也是在笔者和室友后期验算时,发现怎么算怎么不对,最后才定位出的问题)。在agent的一次action中,它会根据最优的action选定一个方向,有0.8的概率按照最优方向行动,有0.1的概率偏向最优方向相对的左侧和右侧。
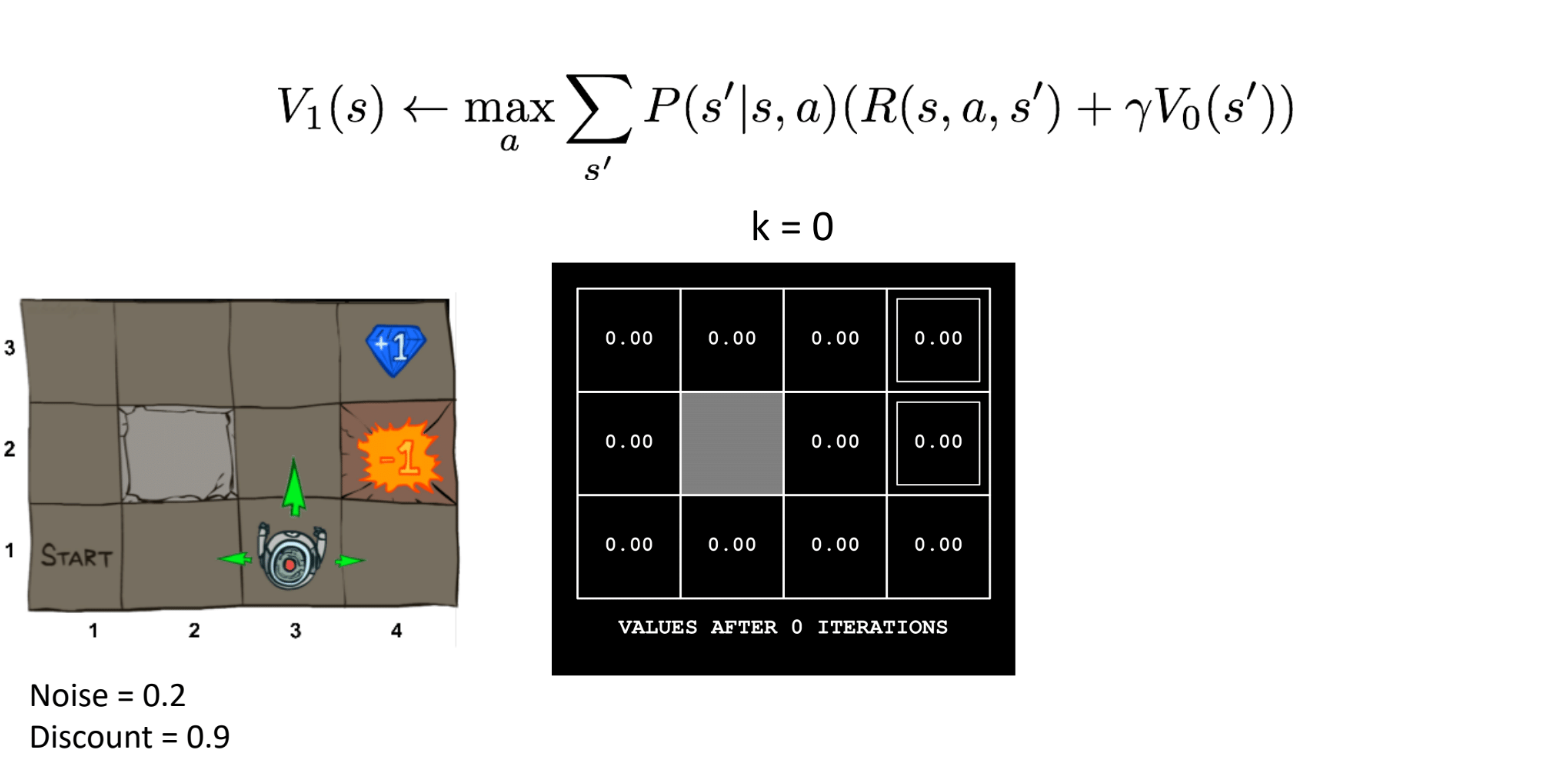
第0次迭代时,所有的
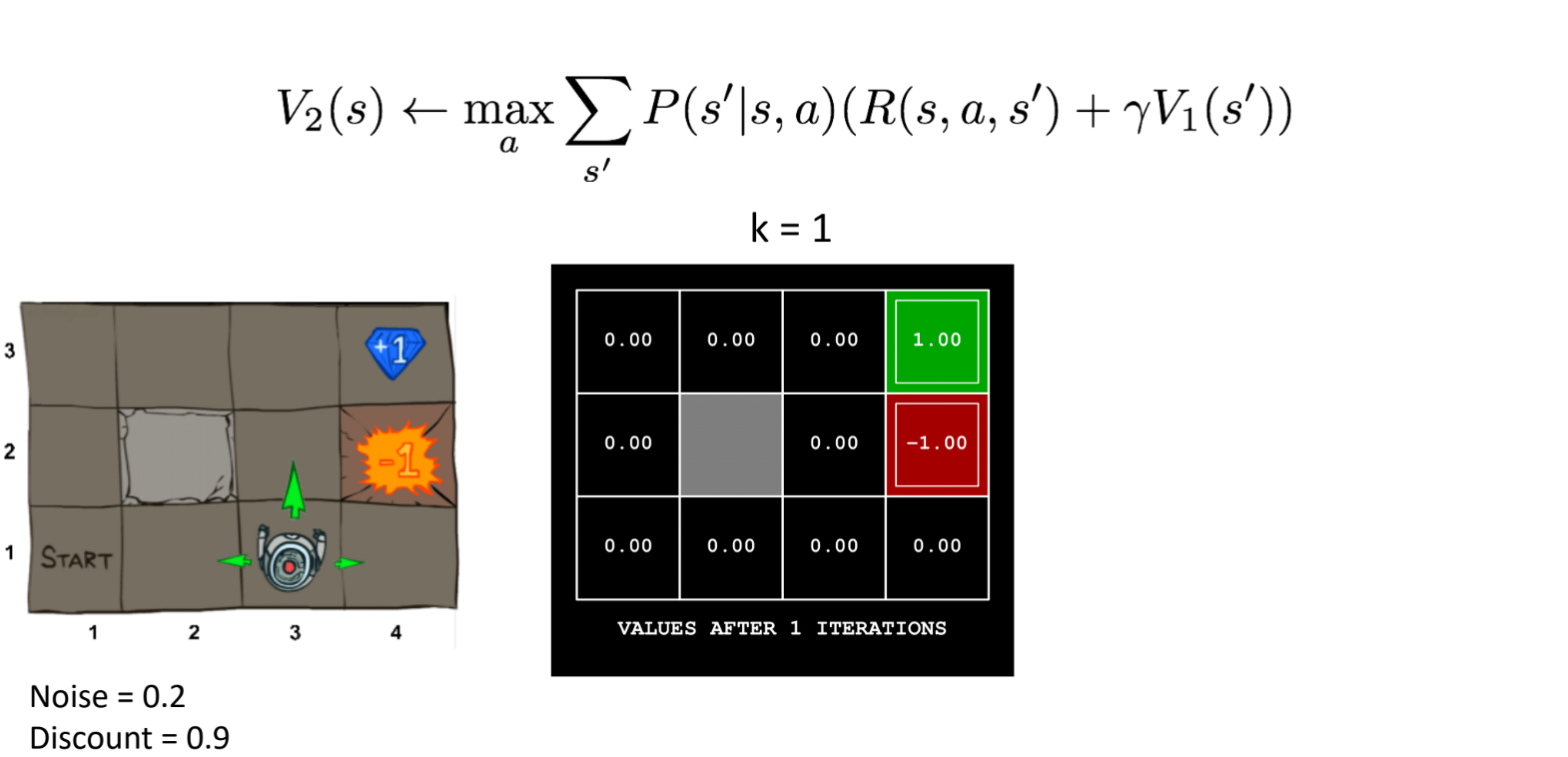
第1次迭代时,有奖励的状态被赋值为相应的奖励值(按照公式计算不知道咋算,按照示例来看应该直接赋值就好)。
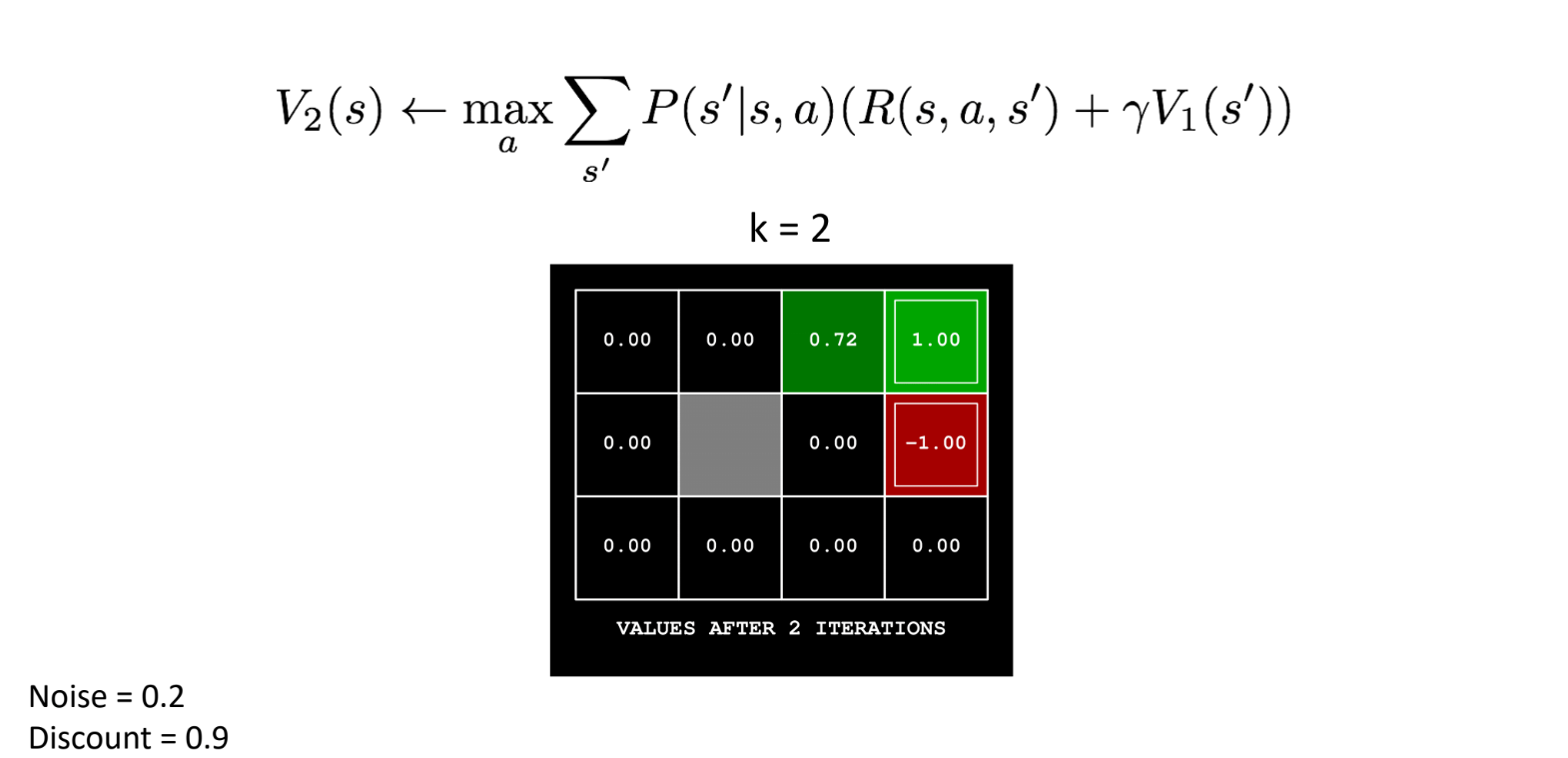
第2次迭代时,则根据上一次迭代的值进行计算(奖励和惩罚区域始终保持不变):
以action肯定是往右: action是向右,所以noise产生的偏差应该是向上或者向下,分别有0.1的概率,而向上撞墙会保持原地。
关于reward,按照例子来看,每一步的奖励始终为0。

第3次迭代时,需要根据公式更新相邻格:

第4次迭代计算过程省略了。只需要记住最优action的方向和可能偏移的方向即可。

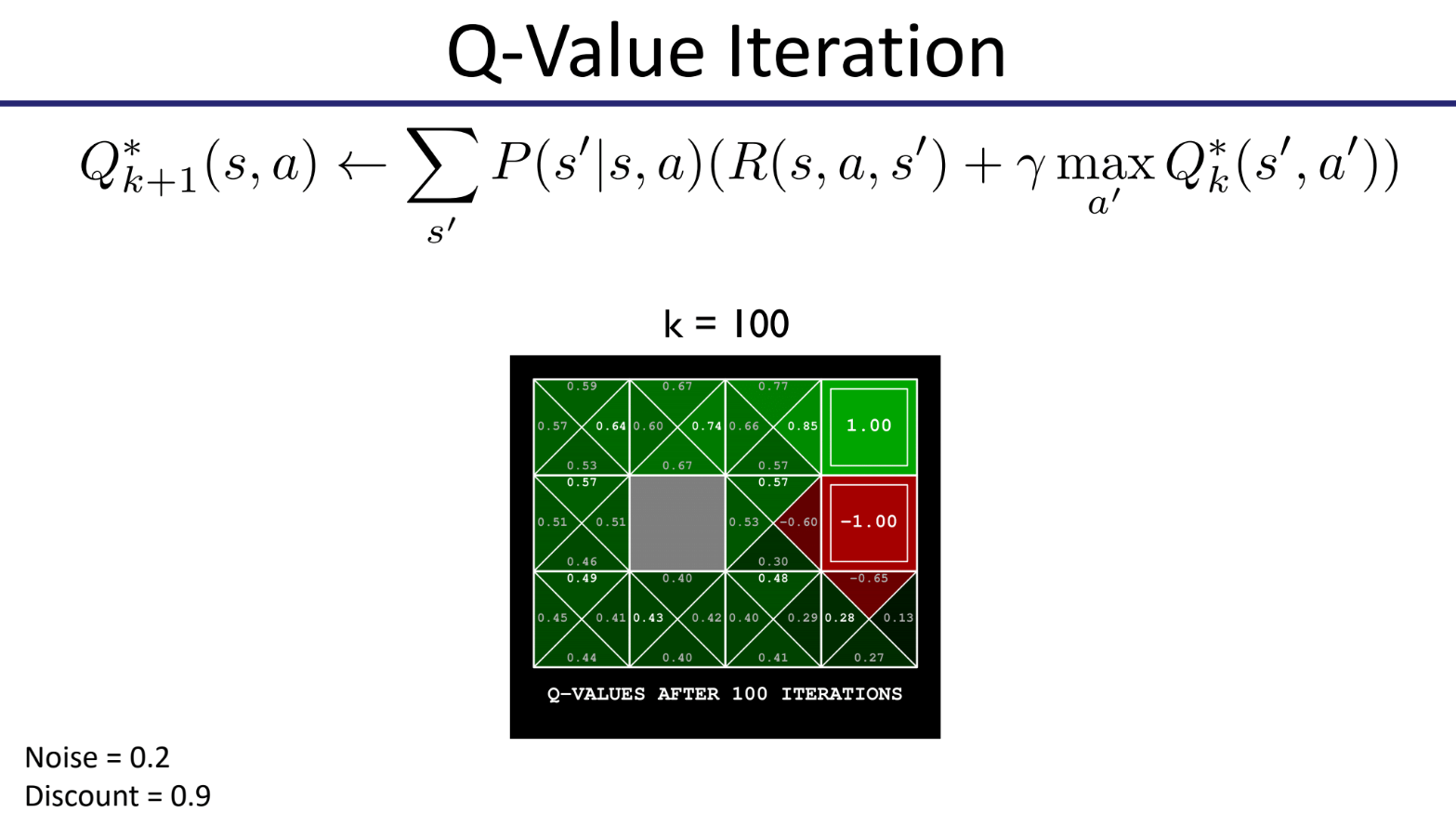
第100次迭代时,值迭代已趋近收敛。
收敛速度往往与折扣因子有关,折扣因子越趋近0,收敛速度越快。
理论:
值迭代总是会收敛。在收敛处,我们能获得带折扣因子的无限期问题的最优值函数
为了获取最优的行动,只需要根据下面步骤执行:
执行值迭代过程,直到收敛。
获得
,通过 反推下一步行动:
无限期策略是稳定的,状态
直觉:
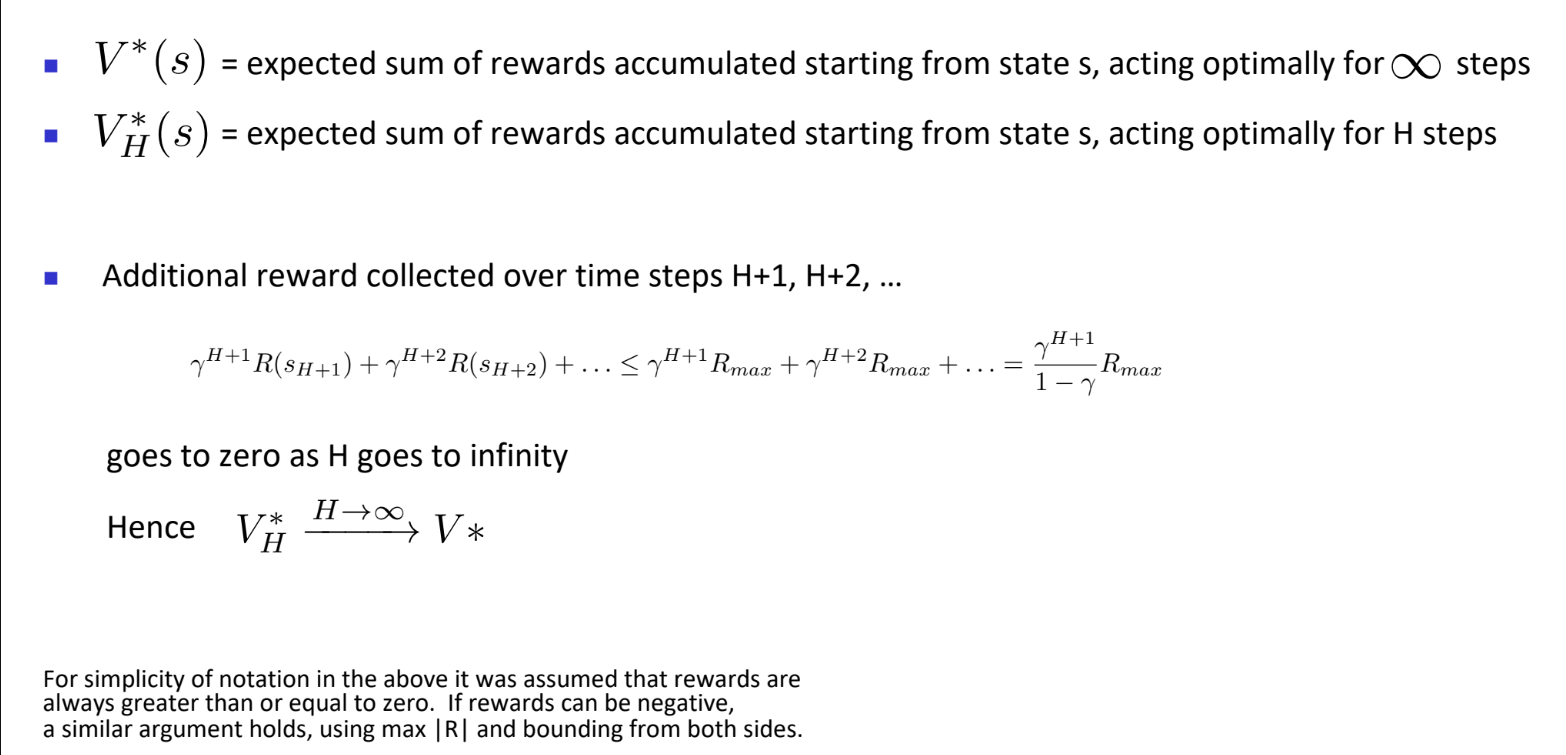
随着范围

定义:Max-Norm(最大范数)
解释:这是最大范数(max-norm,也叫∞-norm)的定义。它表示向量
定义:γ-压缩映射(γ-Contraction)
一个更新操作是 max-norm 下的 γ-压缩映射,当且仅当:
解释:这是“压缩映射”的定义。它说明更新操作会将任意两个输入的差异(在 max-norm 下)收缩最多 γ 倍。如果
定理:压缩映射必收敛到唯一不动点
Banach Fixed Point Theorem(巴拿赫不动点定理)
如果一个映射是压缩映射(在完备空间中),则存在唯一不动点,并且从任意初始点迭代最终都收敛于它。
事实:值迭代是一个 γ-压缩映射
令Bellman更新操作,即:
我们可以证明:
推论:值迭代收敛到唯一固定点
因为值迭代是 γ-压缩映射,根据不动点定理,值函数会收敛到唯一固定点 (
补充事实:误差界估计(用于停止条件)
若满足:
则有:
解释:这个不等式用于衡量我们与最优值函数
- 意思是:如果连续两次更新的差距已经很小(小于 ε)了,那么我们离最终解
也不会太远。
(二)、策略迭代
不同于
最优 Q 值的贝尔曼方程:
- 外层是对所有可能下一状态
的期望; :从 执行动作 到达 的概率; :即时奖励; :折扣因子; :表示在下一个状态 采取最优动作的最大回报。
这是“先拿奖励,再考虑未来的最优行为”的形式。
Q值迭代:
每一步更新 Q 值时,使用当前的
来近似未来的最大期望回报,重复迭代直到收敛为 。
示例 点击展开查看
策略评估:
回顾上面的值迭代:

策略迭代:
策略迭代由两大步骤组成,并反复进行直到策略收敛:
1. 策略评估(Policy Evaluation)
给定当前策略
- 不断迭代直到
收敛;
2. 策略改进(Policy Improvement)
用当前的值函数
这个“评估-提升”的循环是保证有效的,它最终一定会停止,并且停止时找到的就是最优策略和最优价值函数。
- (1) 保证收敛 (Guarantee to converge)
- 每次“策略提升”,新策略要么比老策略好,要么和老策略一样好(在已经达到最优的情况下)。它永远不会变得更差。
- 因为策略总是在变好(或者不变),所以除非已经达到最优,否则你不会重复遇到同一个策略。
- (2) 收敛即最优 (Optimal at convergence)
- 算法收敛(停止)的标志是:在“策略提升”那一步,发现新策略和老策略一模一样了,没有任何改进空间了。
- 这意味着对于每个状态,当前策略
所选择的动作,本身就已经是那个能最大化“下一步期望价值”的动作了(也就是满足了策略提升 的条件)。
最大熵公式
次优解分布:
传统的RL算法(比如我们上面讨论的Policy Iteration)通常致力于找到一个唯一的、最好的策略
- 更鲁棒的策略 (More robust policy)
如果环境发生变化,这个次优解的集合中,可能仍然有适用于新情况的好解法。
- 问题:如果你只知道那条唯一的“最快路线”,万一这条路上突然发生了交通事故(环境变化),你就懵了,不知道该怎么办。你的策略瞬间失效。
- 解决方案:如果你有好几条备选的“优秀路线”,当主路线堵车时,你可以立刻从中选择另一条路绕过去。你的整体策略对意外情况的抵抗能力(即鲁棒性)就大大增强了。
- 在RL中,一个只学习到最优策略
的智能体,在环境发生微小变化时(例如,某个关键路径被阻挡),可能会表现得非常糟糕。但如果它掌握了多个次优策略,它就能快速适应,从“备用方案”中拿出一个来执行,表现得更加稳定和可靠。
- 更鲁棒的学习过程 (More robust learning)
如果我们能保持一个次优解的集合,我们的智能体在学习过程中就能收集到更有价值的探索数据。
这主要关乎“探索与利用 (Exploration-Exploitation) ”的权衡问题。
- 问题:智能体为了学习,不能只执行它当前认为最好的动作(利用),也需要尝试一些未知的动作来发现可能更好的新策略(探索)。但怎么探索是个大学问。
- 解决方案:如果智能体心中有好几个“优秀解法”,它的探索就可以是“在这些优秀解法之间进行尝试”。
- 通过这种方式,智能体收集到的数据都是来自于“高水平尝试”,数据质量非常高。这可以帮助它学得更快、更稳定,并且避免过早地锁定在某个局部最优解上,从而更容易找到全局最优解。
熵:
定义一:熵是随机变量X不确定性的度量 (measure of uncertainty)。
定义二:熵是(平均而言)编码随机变量X所需要的比特数 (number of bits required to encode X)。
数学公式:
:代表整个随机事件”。 :代表一个具体的可能结果。 :代表结果 xi 发生的概率。 :它代表了单个结果 发生时所包含的“信息量”。 - 如果一个事件概率很高,p(xi)→1,那么 log2p(xi)→0。这件事发生不意外,信息量为0。
- 如果一个事件概率很低,p(xi)→0,那么 log2p(xi) 是个很大的负数,所以 −log2p(xi) 就是个很大的正数。这件事的发生非常意外,信息量巨大!
- ∑ip(xi)…:最后,我们把每个可能结果的“信息量”乘以它自己发生的“概率”,然后全部加起来。这其实就是在计算整个事件X的“平均信息量”或“平均意外程度”,也就是熵。
最大熵MDP:

在常规的MDP公式的基础上,引入了熵的参数。新引入的内容会观察策略的熵。
约束优化:

在约束优化中,我们会在一些约束条件下求解最值问题。比如在
为了求解,我们引入拉格朗日函数,并改为求如下值:
拉格朗日原理概述 点击展开查看
拉格朗日原理概述:
问题设定:
- 我们希望最大化或最小化一个目标函数
。 - 同时,必须满足一个或多个约束条件
。
- 我们希望最大化或最小化一个目标函数
拉格朗日函数:
为了将约束条件引入到优化问题中,我们构造拉格朗日函数:
这里,
是拉格朗日乘子,用于调整约束的影响。
求解步骤:
对拉格朗日函数进行偏微分,得到以下条件:
第一个条件指示在优化点上,函数的变化率为零;第二个条件确保约束条件被满足。
几何解释:
- 几何上,优化问题可以看作是在某个函数的等高线(或曲面)上寻找最优点,而约束条件则像是这条等高线与某个边界的交点。拉格朗日乘子帮助我们找到这些交点。

1. 目标函数
最大化期望奖励和策略熵的加权和。熵代表策略的随机性,
2. 约束条件
策略
3. 求解方法
这是一个带约束的优化问题,使用拉格朗日乘子法。构造拉格朗日函数
4. 最终解
最优策略的形式是一个 Softmax 分布。奖励越高的动作,被选中的概率就呈指数级越高。 
紧接上一步,开始计算我们找到的最优策略所对应的最优价值(Optimal Value, V)。
回顾价值公式:
接着,将上一页推导出的最优Softmax策略
化简得到最终结果:

在此基础上,我们希望把我们之前讨论的单步最大熵解法,推广到了更普遍的多步强化学习问题中。
这个算法是一种基于动态规划的递归方法。在还剩
- 执行一个动作
后获得的即时价值 - 进入下一个状态
后,在剩下 步中所能获得的价值。
这就得到了最大熵贝尔曼方程:
既然问题结构相同,我们就可以直接套用单步问题的解,只需把
- 标题: MDPs and Exact Solution Methods
- 作者: Felix Christian
- 创建于 : 2025-06-16 14:28:05
- 更新于 : 2025-07-14 01:03:29
- 链接: https://felixchristian.top/2025/06/16/16-DeepRL_lecture1/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。